Inverted Pendulum Control System Design

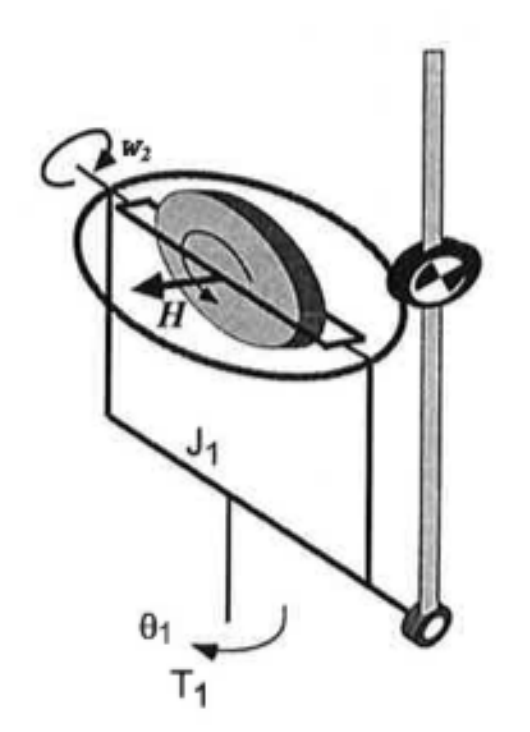
In a postgraduate elective on applied control, METR6203, we were asked to develop a feedback control system to swing-up and balance and inverted pendulum using Matlab and Simulink for modelling and the plant ECP 750 for testing.

Implementing the solution required understanding a number of concepts from stability theory, signal processing and modelling of dynamics.

The Inverted Pendulum Problem

Balancing an inverted pendulum is a very old and studied problem, as it requires to consider non-linear system dynamics control.

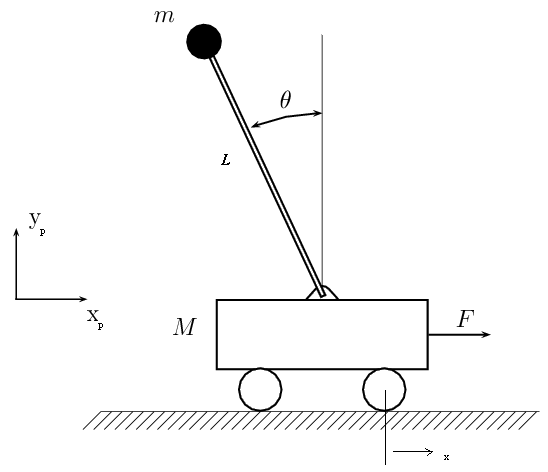
The when the pendulum is close to its equilibrium point, the system can be approximated as linear; however, if the system is initially at rest with the pendulum hanging, this assumption no longer holds true.

Swing-Up Phase

Lyapunov Function

During swing up, in which the system is conditionally stable, a Lyapunov control function is implemented to accelerate the pendulum. When the pendulum reaches the top position, state-space control transition is triggered during which the system is controlled based on a linear approximation.

With the linear approximation in mind, the dynamics of the pendulum in the system above, reduce to:

$$\frac{d^2\ddot{\theta}}{dt^2} = \sin\theta + u\cos\theta$$

Where $u$ is a arbitrary control input. This allows us to rearrange for the derivative of the system’s energy:

$$\frac{dE}{dt}=-\frac{d\theta}{dt}sin\theta + \frac{d\theta}{dt}\frac{d^2\theta}{dt^2}$$

$V$ is a proposed Lyapunov function with $E$ being the system energy.

$$V = \frac{1}{2}(E - E_0)^2$$

Substituting the system’s energy derivative yields the Lyapunov function gradient.

$$\frac{dV}{dt} = (E-E_0)\frac{d\theta}{dt}(u \cos\theta)$$

By measuring or simulating the angular displacement $\theta$ from the top position, Lyapunov gradient is evaluated in real time, and used as a control input to the quasi-linear gyroscopic torquer system. This is used to accelerate pendulum to a position with minimal error from the top equilibrium point.

When the pendulum reaches the equilibrium point, a finite state machine is used to hand the control over to the linear quadratic regulator (LQR).

Linear Quadratic Regulator

Since the gyroscope mounted pendulum is a 2-DoF system, a multiple-input-multiple-output (MIMO) controller is required. The state-space representation of the system is given below, where $x = [\theta \dot{\theta} \gamma \dot{\gamma} \psi \dot{\psi}]$, with $\theta$ being pendulum angle, $\gamma$ being gimbal angle, and $\psi$ being table angle.

$$\dot{x} = Ax + Bu$$

In theory of optimal control, we want to operate a system at minimum cost. This can be done by using a linear quadratic regulator, a feedback controller design algorithm that minimises a cost function often expressed as $J$ in the Riccatti equation.

$$J = x^T(t_1)F(t_1)x(t_1) + \int\limits_{t_0}^{t_1} \left( x^T Q x + u^T R u + 2 x^T N u \right) dt$$

The desired behaviour of the system is achieved by iteratively adjusting the cost matrix, $Q$, and verifying the system response through simulation.

Swing and Catch Simulation

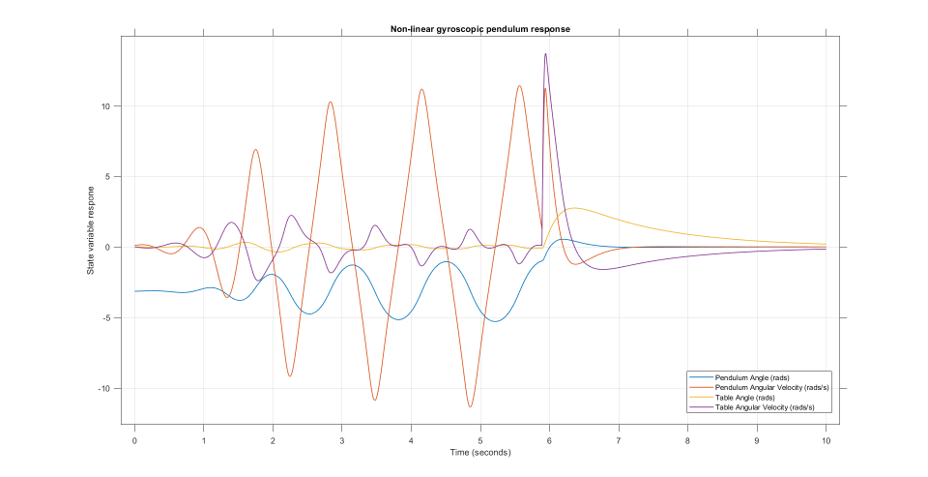
Given a small initial displacement of the pendulum from the hanging equilibrium position, the system will swing up and balance the pendulum. As shown in the plot below, it takes roughly 7 seconds for the system to swing the pendulum up and balance it, and another 3 seconds to bring it to the initial table position.

Controlling Yaw

One of the criteria requires the system to return the pendulum to the initial position with regards to yaw angle (around the vertical axis).

This is done by tuning the LQR parameters so that the controller parameters corresponding to each of the coordinates (table and pendulum angle) are stable individually. The superposition principle allows the overall system to be stable as well.

Demo

Here are two videos demonstrating the control system constructed by my team.